📙[Algo] 24.05.07 알고리즘

알고리즘 문제) BOJ 16947. 서울 지하철 2호선

• 링크 : https://www.acmicpc.net/problem/16947

문제 요약

• 서울 지하철 2호선에는 51개 역이 존재하고, 역과 역 사이를 연결하는 구간이 51개 존재
  • 즉, 정점이 51개, 양방향 간선 51개인 그래프
• 지선 2개, 순환선 1개인 노선도가 주어졌을 때, 각 역과 순환선 사이 거리 구하기
  • 예시 그림
    

    

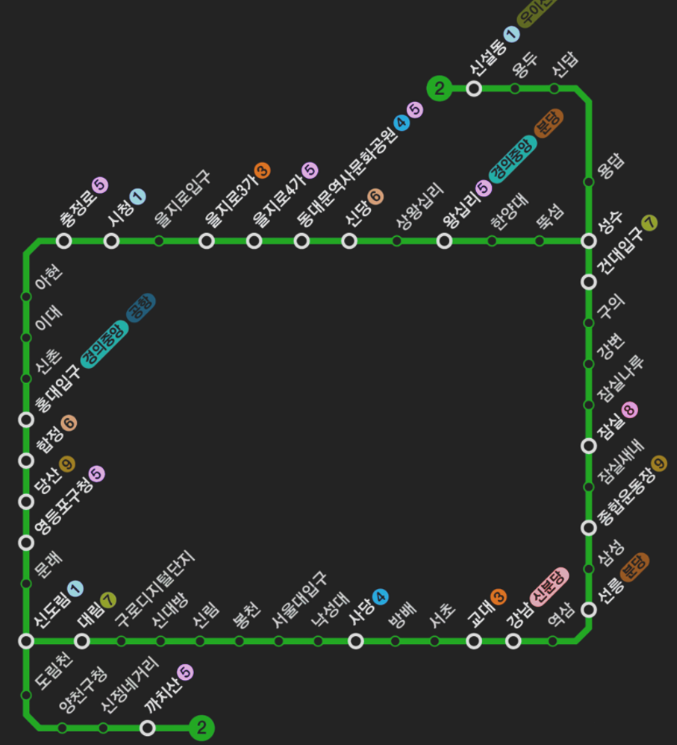
  • 순환선 : 한 역에서 출잘해 다시 출발지로 도착할 수 있는 노선
  • 거리 : 지나야 하는 구간(간선)의 개수
  • 역A와 순환선 사이 거리 : 역A와 순환선에 속한 역 사이 거리 중 최솟값.

 

시간 제한

• 2초

입력

• 역의 개수 N
  • 3 ≤ N ≤ 3000
• 둘째줄부터 N개의 줄에 구간 정보가 주어짐
  • 역1, 역2
  • 같은 구간 여러번 X
  • 역은 1~~N까지 번호가 매겨져 있음

출력

• 총 N개의 정수를 한 줄에 공백을 두고 출력
  • 1번 역과 순환선 사이의 거리, 2번 역과 순환선 사이의 거리, ..., N번 역과 순환선 사이의 거리

접근법

• 사이클인지 찾기 ⇒ dfs
  • return 값을 boolean으로해서 해당 노드가 싸이클일 경우 true를 반환한다.
  • 사이클 판단 방법
    • 사이클은 노드 개수가 최소 3개 이상이어야 함 → 즉 깊이가 2보다 클 것(간선 개수 2개 이상)
    • 매개변수는 현재 노드 번호(cur), 출발지(start), 깊이(depth)로 구성
    • 깊이가 2보다 크면서 현재 노드와 연결된 다음 노드(nxt)가 출발지(start)와 같다면 사이클이므로 return true를 한다.
    • 재귀를 돌면서 return값이 true인 경우 계속 true를 반환하도록 if 조건문에 함수 호출 넣기
  • 사이클일 경우 set에 노드 번호를 담아주었다.
• 사이클과의 거리 구하기 ⇒ bfs
  • bfs 돌면서 연결된 노드들을 거리(깊이) 별로 큐에 담아준다. → 같은 거리는 큐에 담겨져 있으므로 size만큼 for문을 돌리고 나서 거리(깊이) + 1을 해준다.
  • 만약 큐에서 꺼낸 노드 번호가 set에 포함되어 있다면(즉, 사이클에 포함된 노드라면) 현재까지의 거리(깊이)를 반환한다.

코드

import java.io.*;
import java.util.*;

public class Main {
    static int N;
    static ArrayList<Integer>[] lst = new ArrayList[3010];
    static boolean[] visited = new boolean[3010];
    static Set<Integer> isCycle = new TreeSet<>();

    static boolean dfs(int cur, int start, int depth) {
        visited[cur] = true;

        for (Integer nxt : lst[cur]) {

            if (nxt == start && depth > 2) {
                return true;
            }

            if (visited[nxt]) continue;

            if (dfs(nxt, start, depth + 1)) return true;
        }

        return false;
    }

    static int bfs(int v) {
        Queue<Integer> q = new LinkedList<>();
        q.offer(v);
        visited[v] = true;

        int cur, size, dist = 0;
        while (!q.isEmpty()) {
            size = q.size();

            for (int s = 0; s < size; s++) {
                cur = q.poll();

                if (isCycle.contains(cur)) {
                    return dist;
                }

                for (Integer nxt : lst[cur]) {
                    if (visited[nxt]) continue;

                    visited[nxt] = true;
                    q.add(nxt);
                }
            }

            dist++;
        }

        return dist;
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        N = Integer.parseInt(br.readLine());

        for (int i = 0; i < 3010; i++) {
            lst[i] = new ArrayList<>();
        }

        int v1, v2;
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            v1 = Integer.parseInt(st.nextToken());
            v2 = Integer.parseInt(st.nextToken());

            lst[v1].add(v2);
            lst[v2].add(v1);
        }

        for (int i = 1; i <= N; i++) {
            if (dfs(i, i, 1)) isCycle.add(i);

            Arrays.fill(visited, false);
        }

        StringBuilder sb = new StringBuilder();
        for (int i = 1; i <= N; i++) {
            sb.append(bfs(i)).append(" ");
            Arrays.fill(visited, false);
        }

        System.out.println(sb);

        br.close();
    }
}

 

알고리즘 문제) BOJ 1600. 말이 되고픈 원숭이

• 링크 : https://www.acmicpc.net/problem/1600

문제 요약

• 말이 되고 싶은 원숭이는 말이 이동하는 방식을 따라하기로 헀다.
• 말은 다음과 같이 이동한다.
  

  

• 참고로 말은 장애물을 뛰어넘을 수 있다.
• 그러나 원숭이는 K번만 위와 같이 움직이고 나머지는 인접한 칸으로만 움직일 수 있다.(상, 하, 좌, 우)
• 원숭이가 맨 왼쪽 위에서 맨 오른쪽 아래까지 가야한다.
• 격자판이 주어졌을 때, 최소 동작으로 시작지점에서 도착지점까지 갈 수 있는 방법을 찾아보자.

시간 제한

• 2초

입력

• 첫째줄에 정수 K가 주어짐
  • 0≤K(정수)≤30
• 둘째줄에 가로길이 W, 세로길이 H가 주어짐
  • 1≤W,H(자연수)≤200
• 그다음 H줄에 걸쳐 W개의 숫자가 주어진다.
  • 0 : 평지, 1 : 장애물
  • 장애물은 이동할 수 없다.
  • 시작점과 도착점은 항상 평지이다.

출력

• 첫째 줄에 원숭이의 동작수의 최솟값을 출력
  • 도착지에 갈 수 없다면 -1 출력

접근법

• visited 배열을 3차원으로 선언했다.
  • 즉, 말처럼 이동을 몇 번 했는지에 따라 각각 다른 차원으로 생각하고 방문체크를 해야한다.
  • ⇒ 말처럼 이동하는 것을 언제 하느냐에 따라 경로가 모두 달라지기 때문에
• 또한, 최단 경로를 구해야 했기에 bfs로 돌렸다.
  • 현재 큐에 담긴 size만큼 for문을 돌린 뒤에 이동 횟수를 담는 변수 totalCnt를 1씩 늘려줬다.

코드

import java.io.*;
import java.util.*;

public class Main {
    static int K; // 원숭이가 말처럼 움직일 수 있는 최소 횟수
    static int W, H; // 가로길이(col) W, 세로길이(row) H
    static int[][] map; // 격자판
    static boolean[][][] visited; // 방문 체크

    // 인접한 칸으로 움직이기(상,하,좌,우)
    static int[] monkDelR = {-1, 1, 0, 0};
    static int[] monkDelC = {0, 0, -1, 1};

    // 원숭이처럼 움직이기
    static int[] horseDelR = {-1, -2, -2, -1, 1, 2, 2, 1};
    static int[] horseDelC = {-2, -1, 1, 2, -2, -1, 1, 2};

    static boolean check(int row, int col, int horseMoveCnt) {
        return 0 <= row && 0 <= col && row < H && col < W && map[row][col] == 0 && !visited[horseMoveCnt][row][col];
    }

    static class Node {
        int row;
        int col;
        int cnt;

        Node(int row, int col, int cnt) {
            this.row = row;
            this.col = col;
            this.cnt = cnt;
        }
    }

    static int bfs(int row, int col) {
        Queue<Node> q = new LinkedList<>();
        q.offer(new Node(row, col, 0));
        visited[row][col][0] = true;

        int crow, ccol, mrow, mcol, horseMoveCnt, size, totalCnt = 0;
        while (!q.isEmpty()) {

            size = q.size();

            for (int s = 0; s < size; s++) {
                crow = q.peek().row;
                ccol = q.peek().col;
                horseMoveCnt = q.poll().cnt;

                if (crow == H - 1 && ccol == W - 1) {
                    return totalCnt;
                }

                // 말처럼 움직이기
                if (horseMoveCnt < K) {
                    for (int dir = 0; dir < 8; dir++) {
                        mrow = crow + horseDelR[dir];
                        mcol = ccol + horseDelC[dir];

                        if (!check(mrow, mcol, horseMoveCnt + 1)) continue;

                        visited[horseMoveCnt + 1][mrow][mcol] = true;
                        q.offer(new Node(mrow, mcol, horseMoveCnt + 1));
                    }
                }

                // 인접한 곳 움직이기
                for (int dir = 0; dir < 4; dir++) {
                    mrow = crow + monkDelR[dir];
                    mcol = ccol + monkDelC[dir];

                    if (!check(mrow, mcol, horseMoveCnt)) continue;

                    visited[horseMoveCnt][mrow][mcol] = true;
                    q.offer(new Node(mrow, mcol, horseMoveCnt));
                }
            }

            totalCnt++;
        }

        return -1;
    }


    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        K = Integer.parseInt(br.readLine());

        st = new StringTokenizer(br.readLine());
        W = Integer.parseInt(st.nextToken());
        H = Integer.parseInt(st.nextToken());

        map = new int[H][W];
        for (int i = 0; i < H; i++) {
            st = new StringTokenizer(br.readLine());

            for (int j = 0; j < W; j++) {
                map[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        visited = new boolean[31][H][W];

        System.out.println(bfs(0, 0));

        br.close();
    }
}

 

알고리즘 문제) BOJ 11779. 최소비용 구하기 2

• 링크 : https://www.acmicpc.net/problem/11779

문제 요약

• N 개의 도시가 존재
  • 1 ≤ N ≤ 1000
• 한 도시에서 출발하여 다른 도시에 도착하는 버스 존재
  • 1 ≤ N ≤ 10만
• 도시 A에서 출발하여 도시B까지 가는데 드는 최소비용과 경로 출력하기
  • 항상 경로 존재

시간 제한

• 1초

입력

• 도시 개수 N
  • 1 ≤ N ≤ 1000
• 버스 개수 M
  • 1 ≤ M ≤ 10만
• 셋째줄부터 M+2줄까지 버스 정보가 주어짐
  • 출발 도시 번호, 도착 도시 번호, 버스 비용
    • 0 ≤ 버스비용(정수) < 10만

출력

• 첫째줄 : 출발 도시에서 도착 도시까지 가는데 드는 최소 비용을 출력
• 둘째줄 : 그러한 최소 비용을 갖는 경로에 포함되어있는 도시의 개수를 출력(출발 도시, 도착 도시 포함)
• 셋째줄 : 최소 비용을 갖는 경로를 방문하는 도시 순서대로 출력

접근법

• 다익스트라 알고리즘을 사용하여 최소 경로 찾기
• 경로 추적을 위해 parent배열에 부모 노드(출발지 노드) 저장
  • route 함수를 통해 도착지 도시부터 경로 역추적 → stack에 담음(LIFO 구조)
  • stack에서 순차적으로 출발지부터 도착지까지 노드들 조회

코드

import java.io.*;
import java.util.*;

public class Main {
    static int N, M;
    static ArrayList<Node>[] lst;
    static PriorityQueue<Node> pq = new PriorityQueue<>();
    static int[] dist;
    static boolean[] visited;
    static int start, end;
    static int[] parent;
    static Stack<Integer> stack = new Stack<>();

    static class Node implements Comparable<Node> {
        int no;
        int cost;

        Node(int no, int cost) {
            this.no = no;
            this.cost = cost;
        }

        @Override
        public int compareTo(Node node) {
            return this.cost - node.cost;
        }
    }

    // 다익스트라 알고리즘 -> 출발지로부터 각 노드까지 최단 비용 값으로 dist배열 갱신
    static void daijk(int v) {
        pq.offer(new Node(v, 0));

        int cur, nxt, nc;
        while (!pq.isEmpty()) {
            cur = pq.poll().no;

            if (visited[cur]) continue;

            visited[cur] = true;

            for (Node node : lst[cur]) {
                nxt = node.no;
                nc = dist[cur] + node.cost;

                // 경로저장 -> 해당 노드의 부모 노드 갱신
                if (dist[nxt] > nc) {
                    dist[nxt] = nc;
                    parent[nxt] = cur;
                }

                pq.offer(new Node(nxt, dist[nxt]));
            }
        }
    }

    // 경로 추적 -> stack에 담기(역추적이기 때문에, lifo구조인 stack에 담음)
    static void route(int v) {

        if (v == 0) return;

        stack.add(v);

        route(parent[v]);
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        N = Integer.parseInt(br.readLine());
        M = Integer.parseInt(br.readLine());

        lst = new ArrayList[N + 1];
        for (int i = 0; i < N + 1; i++) {
            lst[i] = new ArrayList<>();
        }

        // 거리 배열
        dist = new int[N + 1];

        // 방문 체크 배열
        visited = new boolean[N + 1];

        // 경로 추적을 위한 부모 배열 
        parent = new int[N + 1];

        int v1, v2, c;
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            v1 = Integer.parseInt(st.nextToken());
            v2 = Integer.parseInt(st.nextToken());
            c = Integer.parseInt(st.nextToken());

            lst[v1].add(new Node(v2, c));
        }

        st = new StringTokenizer(br.readLine());
        start = Integer.parseInt(st.nextToken());
        end = Integer.parseInt(st.nextToken());

        Arrays.fill(dist, 1 << 30);
        dist[start] = 0;

        // 다익스트라 알고리즘 
        daijk(start);

        // 목적지까지 최소 비용 출력
        System.out.println(dist[end]);

        // 경로 추적
        route(end);

        // 목적지까지 거치는 노드 개수 출력
        System.out.println(stack.size());

        // 출발지부터 도착지까지 최단 경로에 속한 노드 출력
        StringBuilder sb = new StringBuilder();
        while (!stack.isEmpty()) {
            sb.append(stack.pop() + " ");
        }
        System.out.println(sb);

        br.close();
    }
}

 

알고리즘 문제) BOJ 1941. 소문난 칠공주

• 링크 : https://www.acmicpc.net/problem/1941

문제 요약

• 25명의 학생으로 이루어진 반에 이다솜파와 임도연파로 갈라짐
• 어느 순간 임도연파가 세력을 확장하였고, 이다솜파는 소문난 칠공주를 결성하기로 함
• 소문난 칠공주 결성 규칙
  • 7명으로 구성
  • 7명의 자리는 서로 가로, 세로 인접할 것
  • 반드시 이다솜파로만 구성될 필요 X
  • 그러나 최소 이다솜파가 4명이상 포함할 것
• 여학생의 자리배치도가 주어졌을 때, 소문난 칠공주를 결성할 수 있는 모든 경우의 수 구하기

시간 제한

• 2초

입력

• 'S'(이다‘솜’파의 학생을 나타냄) 또는 'Y'(임도‘연’파의 학생을 나타냄)을 값으로 갖는 5*5 행렬이 공백 없이 첫째 줄부터 다섯 줄에 걸쳐 주어진다

출력

• 첫째 줄에 ‘소문난 칠공주’를 결성할 수 있는 모든 경우의 수를 출력

접근법

• 처음에 2차원으로 백트랙킹 돌리려니 중복으로 카운트되는 문제가 생겼다.
• 그래서 2차원을 1차원으로 펼치기로 했다.
  • 1차원 인덱스(번호) = 5*행번호(row) + 열번호(col)
    • 즉, 1차원으로 펼쳐서 좌석 번호를 부여했을 때, 좌석번호를 5로 나눈 몫이 행값이 되고, 난머지가 열값이 된다.
• 0~24중에서 7개를 중복없이 선택하게 함 ⇒ 조합(comb 메소드)
  • 이때, arr[좌석번호/5][좌석번호%5]가 “Y”라면 임도연파 개수 + 1을 하고 넘긴다.
    • 임도연파인 학생은 최대 3명까지 가능하기 때문에 체그해야함
  • 7개를 모두 선택했을 때, 임도연파 학생 수가 4명 미만일 경우에만 선택한 학생들이 인접하게 앉아있는지 판단 → 맞다면 answer + 1
• 인접했는지 체크하기 ⇒ bfs
  • 우선 set에다가 선택한 좌석 번호들을 담았다. ⇒ 추후에 bfs돌리면서, 선택한 좌석만 큐에 담기 위해
  • bfs돌리면서 인접한 애들 중에 set에 있는 애들만 큐에 담으며, cnt+1함
  • cnt가 7일 경우에만 return true

코드

import java.io.*;
import java.util.*;

public class Main {
    static char[][] arr = new char[5][5];
    static int[] selected = new int[7];
    static Set<Integer> set = new TreeSet<>();
    static Queue<Integer> q = new LinkedList<>();
    static boolean[] visited = new boolean[25];
    static int[] delR = {1, 0, -1 ,0};
    static int[] delC = {0, 1, 0 , -1};
    static int answer = 0;

    // 자리 선택하기 -> 중복이 있으면 X -> 따라서 조합
    static void comb(int cur, int start, int yCnt) {

        if (cur == 7) {
            // 임도연이 3명이하인 경우만 가능하므로
            if (yCnt < 4) {
                // 인접한 좌석이라면 answer증가
                if (isNear()) answer++;
            }
            return;
        }

        for (int i = start; i < 25; i++) {
            selected[cur] = i;

            // 임도연이라면 yCnt를 하나 증가시켜주기
            if (arr[i / 5][i % 5] == 'Y') {
                comb(cur + 1, i + 1, yCnt + 1);
            } else {
                comb(cur + 1, i + 1, yCnt);
            }
        }

    }

    static boolean isNear() {
        int cnt = 1;

        // 선택한 좌석인지 체크하기 위해 set에 담음
        for (int i = 0; i < 7; i++) {
            set.add(selected[i]);
        }

        // 좌석 하나 담고 시작하고
        q.offer(selected[0]);
        visited[selected[0]] = true;

        int cur, crow, ccol, mrow, mcol;
        while (!q.isEmpty()) {
            cur = q.poll();

            // 1차원 인덱스 2차원 인덱스로 바꾸기
            crow = cur / 5;
            ccol = cur % 5;

            // 인접한 곳으로만 이동한다.
            for (int dir = 0; dir < 4; dir++) {
                mrow = crow + delR[dir];
                mcol = ccol + delC[dir];

                // 경계 및 방문 체크
                if (mrow < 0 || mcol < 0 || 5 <= mrow || 5 <= mcol || visited[mrow * 5 + mcol]) continue;

                // 선택한 좌석인지 체크
                if (!set.contains(mrow * 5 + mcol)) continue;

                // 인접하면서 선택된 좌석이라면..
                visited[mrow * 5 + mcol] = true;
                q.offer(mrow * 5 + mcol);
                // 인접 개수 증가
                cnt++;
            }
        }

        // 초기화
        q.clear();
        set.clear();
        Arrays.fill(visited, false);

        // 인접한 개수 cnt가 7개면 return true
        if (cnt == 7) return true;
        else return false;
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        String input;
        for (int i = 0; i < 5; i++) {
            input = br.readLine();

            for (int j = 0; j < 5; j++) {
                arr[i][j] = input.charAt(j);
            }
        }

        // 2차원을 1차원으로 펼치기 -> row * 5 + col -> 몫이 row값, 나머지가 col값
        // 1차원 인덱스를 2차원으로 바꾸기 row : (1차원 인덱스 값)/5 , col : (1차원 인덱스 값)%5
        comb(0, 0, 0);

        System.out.println(answer);

        br.close();
    }
}