📙 Algorithm Solving/Java
📙[Algo] 24.05.23 알고리즘
혜덕hyeduck
2024. 5. 24. 01:02
알고리즘 문제) BOJ 3114. 사과와 바나나
문제 요약
- R*C맵에 A나라와 B나라가 존재
- 각 칸에는 A나무(사과) 개수, B나무(바나나) 개수가 주어짐
- (1,1)부터 시작해 (R,C)까지 불도저를 이동하면서 나무를 제거하고, 국경선을 만들려고함
- 이때 국경선 아래는 A, 국경선 위는 B국가가 가지게 되는데,
- A나라는 사과를 좋아하고, B나라는 바나나를 좋아한다.
- 따라서, 국경선 아래에 사과나무 개수 합과 국경선 위의 바나나 나무 개수 합이 최대가 되는 경우를 찾을 것
시간 제한
- 1초
입력
- 땅의 크기 R,C ( 2 ≤ R,C ≤ 1500)
- R개의 줄에 각 칸에 심어져 있는 나무 개수가 주어짐
- 사과는 A, 바나나는 B이며 심어져 있는 나무 개수는 1~99
출력
- 가능한 합 중 가장 큰 것 출력
접근법
- 탑다운 dp + 누적합
- 국경선기준 위는 바나나 개수 총합을 구해야하고 아래는 사과 개수 총 합을 구해야 함.
- 이때, 이동했을 때, 확실히 영토가 확정되는 경우를 파악
- 이동을 오른쪽, 아래, 오른쪽 아래 대각선으로만 이동 가능하다는 점을 생각했다.
- 오른쪽 이동 시, 이전 위치의 아래 칸들은 A 영토로 확정

- 아래 이동 시, 이전 위치의 오른쪽 칸들은 B영토로 확정.
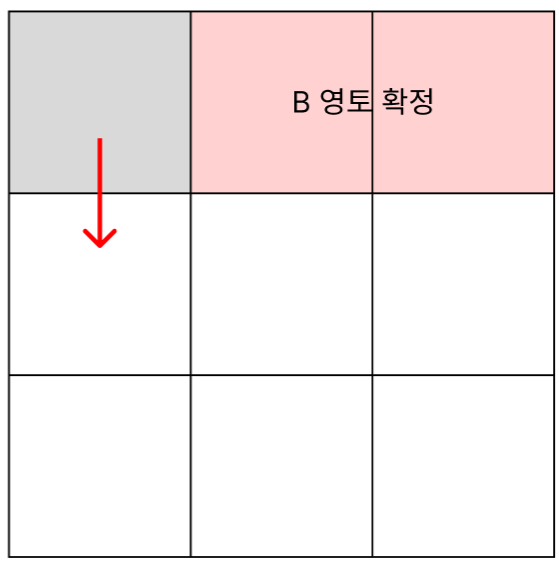
- 오른쪽 아래 대각선 이동 시, 위의 두 케이스처럼 A영토, B영토가 동시에 확정된다.

- 그래서, 확정된 만큼 apple또는 banna 합계를 더해줬다.
- 또한, 일일이 매케이스마다 합계를 구하지 않고, 누적합 배열을 만들어서 사용했다.
- apple누적합 배열은 → 세로 누적
- banana누적합 배열은 → 가로 누적
코드
import java.io.*;
import java.util.*;
public class Main {
static int R, C;
static int[][] banana;
static int[][] apple;
// 아래, 오른쪽, 오른쪽 대각선 아래
static int[] delR = {1, 0, 1};
static int[] delC = {0, 1, 1};
static int[][] dp;
static int recur(int row, int col) {
if (row == R && col == C) return 0;
if (dp[row][col] != -1) return dp[row][col];
int mr, mc, ret = 0;
for (int dir = 0; dir < 3; dir++) {
mr = row + delR[dir];
mc = col + delC[dir];
if (R < mr || C < mc) continue;
if (dir == 0) {
// 아래 이동 시, 즉 mr가 1칸 아래로 옮기면 bSum += banana[row][C] - banana[row][col]
ret = Math.max(ret, recur(mr, mc) + banana[row][C] - banana[row][col]);
} else if (dir == 1) {
// 오른쪽 이동 시, 즉 mc가 1칸 뒤로 옮기면 aSum += apple[R][col] - apple[row][col]
ret = Math.max(ret, recur(mr, mc) + apple[R][col] - apple[row][col]);
} else {
// 오른쪽 아래 대각선 이동 시, aSum += apple[R][col] - apple[row][col], bSum += banana[row][C] - banana[row][col]
ret = Math.max(ret, recur(mr, mc) + banana[row][C] - banana[row][col] + apple[R][col] - apple[row][col]);
}
}
dp[row][col] = ret;
return ret;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
R = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
banana = new int[R + 1][C + 1];
apple = new int[R + 1][C + 1];
String str; char tree; int cnt;
for (int i = 1; i <= R; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= C; j++) {
str = st.nextToken();
tree = str.charAt(0);
cnt = Integer.parseInt(str.substring(1));
if (tree == 'B') {
banana[i][j] = cnt;
} else {
apple[i][j] = cnt;
}
}
}
// 2차원 누적합 배열 만들기
// 바나나 -> 행별로 가로 누적
for (int r = 1; r <= R; r++) {
for (int c = 1; c <= C; c++) {
banana[r][c] += banana[r][c - 1];
}
}
// 사과 -> 열별로 세로 누적
for (int c = 1; c <= C; c++) {
for (int r = 1; r <= R; r++) {
apple[r][c] += apple[r - 1][c];
}
}
dp = new int[R + 10][C + 10];
for (int[] d : dp) {
Arrays.fill(d, -1);
}
System.out.println(recur(1, 1));
br.close();
}
}
알고리즘 문제) BOJ 2281. 데스노트
문제 요약
- 순서가 정해진 N명의 이름이 있다.
- 순서대로 노트 위→아래, 왼→오른쪽 으로 차례대로 적는다.
- 이름 사이에는 빈 칸을 하나씩 둬야함
- 만약, 중간에 이름이이 잘린다면, 반드시 새로운 줄에 이름을 적어야 한다.
- 이때 이때, 각 줄의 끝에 사용하지 않고 남게 되는 칸의 수의 제곱의 합이 최소가 되되는 경우 찾기
시간 제한
- 2초
입력
- 사람 수 N 노드 가로 칸 수 M
- 1 ≤ N ≤ 1000
- 1 ≤ M ≤ 1000
- N개의 줄에 각 사람의 이름의 길이가 노트에 적어야 할 순서대로 주어진다
출력
- 첫째 줄에 남게 되는 칸 수의 제곱의 합의 최솟값을 출력
접근법
- 탑다운 dp로 풀었다.
- 문제 잘 읽기 → 적어야할 이름 순서는 정해져 있음
- 결국, 케이스가 나뉘는 거는 해당 행에 현재 이름을 적느냐 안적느냐
- cur는 현재 가리키는 이름 인덱스
- remain은 현재 행의 남은 칸수를 넘기는 변수인데, 이름마다 한 칸씩 띄워야 하므로 1을 추가로 더 뺴줬다.
- ⇒ 그래서 나중에 남은 공간 제곱합 더할때 remain + 1을 제곱해서 더해야함(마지막 이름 넘길때 1칸 뺐으므로)
- 현재 행에 이름을 적는 경우
- 남은 칸에 이름 길이 + 1(공백)만큼 뺀다. remain - arr[cur] - 1
- 현재 행에 안 적을 경우
- remain을 M - arr[cur] - 1로 바꿈 → 새로운 행으로 교체되었으므로 M에서 뺀다.
- remain+1을 제곱한만큼 답에 더해줌
- 위 두케이스의 반환값중 최솟값을 return하도록 함.
- 그리고 가지치기가 중요한데, 만약 remain값이 음수일 경우 불가능 한 케이스이므로 답이 될 수 없도록 가장 큰 값을 반환시켰다.
- 이때 0미만이 아니라 -1미만인 이유는, remain을 넘길 때 공백을 염두에두고 1을 추가로 더뺐기 때문
- 그래서 remain이 -1인 경우도 가능한 케이스이므로 dp메모이제이션 할 때는 remain + 1인덱스를 조회하도록 변경함
코드
import java.io.*;
import java.util.*;
public class Main {
static int N, M;
static int[] arr;
static int[][] dp;
static int recur(int cur, int remain) {
// 가지치기 -> -1미만인 이유 -> remain 넘길떄 1을 더 빼고 넘기고 있어서
if (remain < -1) return 1 << 30;
if (cur == N) return 0;
// remain+1한 이유는 이 자리에 -1이 올 수 있어서
if (dp[cur][remain + 1] != 1 << 30) return dp[cur][remain + 1];
int ret = 1 << 30;
// 현재 행에 적는경우
ret = Math.min(ret, recur(cur + 1, remain - arr[cur] - 1));
// 현재 행에 적지 않는 경우
ret = Math.min(ret, recur(cur + 1, M - arr[cur] - 1) + (int) Math.pow(remain + 1, 2));
dp[cur][remain + 1] = ret;
return ret;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
arr = new int[N];
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
dp = new int[N + 1][1100];
for (int[] d : dp) {
Arrays.fill(d, 1 << 30);
}
System.out.println(recur(0, M));
br.close();
}
}
알고리즘 문제) BOJ 26215. 눈 치우기
문제 요약
- 1분마다 한 집 또는 두 집 앞의 눈을 각각 1만큼 치울 수 있음
- 모든 집 앞 눈을 전부 치우는데 걸리는 최소 시간은?
시간 제한
- 1초
입력
- 집의 수를 의미하는 정수 N(1 <= N <= 100)
- 각각 집 앞에 쌓여 있는 눈의 양 ai (1 <= ai <= 2000)
출력
- 모든 집 앞 눈을 치우는데 최소 몇 분?(24시간(1440분) 넘는다면 -1출력)
접근법
- 그리디적으로 접근했다. → 유사문제 비드맨
- 일단 최대한 최소시간으로 눈을 치우려면 두 개의 집을 동시에 치우는 경우가 제일 많은 케이스를 찾아야한다.
- 즉, 눈의 양이 골고루 감소되어야 한다.
- 결국 가장 최대로 쌓여있는 눈의 양이 기준이 되는데,
- 해당 눈의 양이 0이 될 때까지 다른 집을 방문하면서 같이 눈을 치우는 경우를 생각해볼 수 있다.
- 그러면, 대충 아래 3가지 케이스가 나옴
- 눈의 양 최대값 == 나머지 눈의 양 합
- 이 경우에는 최대값을 다른 눈이랑 같이 감소시키다보면 결국 최대값만큼 시간이 소모됨 → 최대값
- 눈의 양 최대값 > 나머지 눈의 양 합
- 우선 최대값을 다른 눈이랑 같이 감소시키고 → 나머지 눈의양 합만큼 시간 소모
- 최대값에서 나머지 눈의 양 뺸 만큼 남게 되는데, 이때 그 눈은 한 집만 갖고 있는 것이므로 추가로 남은 눈의 양만큼 더해줌 → 최대값 - 나머지 눈의양 합
- 눈의 양 최대값 < 나머지 눈의 양 합
- 여기서 좀 고민을 많이 했다.
- 우선 최대값을 다른 눈이랑 같이 치우면서 0으로 만드는 시간 소모 → 최대값
- 그럼 나머지 눈의 양 합 - 최대값 만큼 남게 되는데, 이 눈들이 집집마다 다르게 갖고 있을 것이다.
- 그런데, 앞에서 생각했듯이 우리는 최대한 골고루 눈을 치우게 되니까, 남은 눈의 양도 집집마다 고르게 분포되어 있을거라 가정할 수 있다.
- 그러면 (나머지 눈의 양 합 - 최대값)/2 만큼 더하고, 추가로 (나머지 눈의 양 합 - 최대값)%2를 더하면 된다.
- (나머지 눈의 양 합 - 최대값)/2 : 두 집을 골고루 치우게 되니까, 몫만큼 더해주고
- (나머지 눈의 양 합 - 최대값)%2 : 만약 1이 남는다면, 이거는 한 집에 눈이 1만큼 남아 있는 경우를 생각해볼 수 있음
- 눈의 양 최대값 == 나머지 눈의 양 합
코드
import java.io.*;
import java.util.*;
// 20분
public class Main {
/*
문제
1분마다 한 집 또는 두 집 앞의 눈을 각각 1만큼 치울 수 있음
모든 집 앞 눈을 전부 치우는데 걸리는 최소 시간은?
입력
집의 수를 의미하는 정수 N(1 <= N <= 100)
각각 집 앞에 쌓여 있는 눈의 양 ai (1 <= ai <= 2000)
출력
모든 집 앞 눈을 치우는데 최소 몇 분?(24시간(1440분) 넘는다면 -1출력)
케이스
1 2 3 -> 나머지 합 == 최대값 -> 최대값이 답
1 3 4 5 -> 나머지합(8) : 최대값(5)
1 3 3 4
1 3 2 3
1 3 1 2
1 3 0 1
1 2 0 0
0 1 0 0
0 0 0 0
1 2 4 4 5 -> 11 > 5
1 2 4 3 4
1 2 4 2 3
1 2 4 1 2
1 2 4 0 1
1 2 3 0 0
1 1 2 0 0
1 0 1 0 0
0 0 0 0 0
2 3 3 4 4 8 16 > 8 : 최대값(8) + (나머지합16-최대값8)/2 + (나머지합16-최대값8)%2
2 3 3 4 3 7
2 3 3 4 2 6
2 3 3 4 1 5
2 3 3 4 0 4
2 3 3 3 0 3
2 3 3 2 0 2
2 3 3 1 0 1
2 3 3 0 0 0
2 2 2 0 0 0
2 1 1 0 0 0
1 0 1 0 0 0
0 0 0 0 0 0
1 2 4 -> 나머지합(3) < 최대값(4) : 나머지합 + (최대값-나머지합)
*/
static int N;
static int[] arr;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
arr = new int[N];
int sum = 0;
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
sum += arr[i];
}
Arrays.sort(arr);
int remain = sum - arr[N - 1];
int max = arr[N - 1];
int ans;
if (remain == max) {
ans = max;
} else if (remain > max) {
ans = max + (remain - max) / 2 + (remain - max) % 2;
} else {
ans = remain + (max - remain);
}
if (ans > 1440) System.out.println("-1");
else System.out.println(ans);
br.close();
}
}
알고리즘 문제) BOJ 14567. 선수과목 (Prerequisite)
문제 요약
- 한 학기에 들을 수 있는 과목 수에 제한 X
- 모든 과목은 매 학기 항상 개설
- 선수 과목이 있는 경우는 해당 과목을 먼저 이수할 것
- 모든 과목에 대해 각 과목을 이수하려면 최소 몇 학기 걸리나?
시간 제한
- 1초
입력
- 과목 수 N, 선수 조건 수 M(N:1~1000, M:0~500000)
- M개의 줄에 선수과목 조건이 A B(A<B입력만 주어짐)
출력
- 1번 과목부터 N번 과목까지 차례대로 최소 몇 학기에 이수할 수 있는지 출력
접근법
- 위상정렬로 접근
- arr리스트 배열에 각 과목별 자식 과목들을 담고,
- cnt배열은 각 과목의 선수과목 개수 카운트
- cnt배열 값이 0인 애들, 즉 선수과목이 없는 애들먼저 큐에 담은 다음, 큐가 빌때까지 아래 로직 실행
- 각 과목별 자식노드의 cnt배열 값을 1씩 차감
- 이때, cnt배열 값이 0인 과목들은 큐에 담아줌
코드
import java.io.*;
import java.util.*;
public class Main {
/*
1. 한 학기에 들을 수 있는 과목 수에 제한 X
2. 모든 과목은 매 학기 항상 개설
3. 선수 과목이 있는 경우는 해당 과목을 먼저 이수할 것
모든 과목에 대해 각 과목을 이수하려면 최소 몇 학기 걸리나?
입력
과목 수 N, 선수 조건 수 M(N:1~1000, M:0~500000)
M개의 줄에 선수과목 조건이 A B(A<B입력만 주어짐)
출력
1번 과목부터 N번 과목까지 차례대로 최소 몇 학기에 이수할 수 있는지 출력
*/
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 과목 수
int M = Integer.parseInt(st.nextToken()); // 선수과목 조건 수
// 선수 과목
ArrayList<Integer>[] arr = new ArrayList[N + 1];
for (int i = 0; i < N + 1; i++) {
arr[i] = new ArrayList<>();
}
int[] cnt = new int[N + 1];
// p : 선수과목
int p, c;
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
p = Integer.parseInt(st.nextToken());
c = Integer.parseInt(st.nextToken());
arr[p].add(c);
cnt[c]++;
}
Queue<Integer> q = new LinkedList<>();
for (int i = 1; i <= N; i++) {
if (cnt[i] == 0) {
q.offer(i);
}
}
int cur, nth = 1, size;
int[] ans = new int[N + 1];
while (!q.isEmpty()) {
size = q.size();
for (int s = 0; s < size; s++) {
cur = q.poll();
ans[cur] = nth;
for (Integer nxt : arr[cur]) {
cnt[nxt]--;
if (cnt[nxt] == 0) q.offer(nxt);
}
}
nth++;
}
StringBuilder sb = new StringBuilder();
for (int i = 1; i <= N; i++) {
sb.append(ans[i]).append(" ");
}
System.out.println(sb);
br.close();
}
}